Research
Ehsan Roohi mainly works on novel and intelligent collision models in the direct simulation Monte Carlo (DSMC) technique framework to make the rarefied flow simulations more accurate and less time-consuming [3]. The collision process is the most sophisticated part of DSMC, which is treated probabilistically [4]. He has demonstrated the shortcomings of conventional collision models [5] and has been developing innovative intermolecular collision paradigms in the framework of the DSMC. In 2015, he improved the “Simplified Bernoulli” trial (SBT) collision model [6] by introducing an intelligent version, [7] and he was the lead developer of a new collision model called the “Generalized Bernoulli” trial (GBT) scheme in 2018 [8].
In 2022, he developed another model, the “Symmetrized and Simplified Bernoulli” trial (SSBT) scheme, [9] that has improved performance compared to previous ones. In the same year, Stefan Stefanov and he suggested a hybrid collision scheme on transient adaptive subcells to treat various types of rarefied gas flows at the hypersonic regime [10]. He has been developing numerical tools to perform simulations of hypersonic space re-entry vehicles, waveriders, and propulsion of arrays of small-scale satellites much faster with high reliability [11]. During his research career, he contributed to developing the very first open-source DSMC code in the framework of OpenFOAM, i.e., dsmcFoam [12]. His next plan is to incorporate physics-informed machine learning and deep learning methods into ab-inito collision models for hypersonic and non-equilibrium flow simulations. He also works on designing next-generation micro-scale pumps and propulsion systems that exploit heat losses and produce propulsion force and flow motion without requiring pressure gradients. This is done using DSMC simulations and is now extended using machine learning. A thin vane immersed in a rarefied gas with a temperature gradient across its surfaces will produce a force that tends to move the vane from the hot side to the cold side. This is the Crookes radiometer. He has been creating and developing novel concepts in thermal ratchet (rather than using the vanes) pumps and propulsion systems using either an intelligent selection of wall reflection properties or surface morphologies [13].
He was the first to demonstrate that the working mechanism of ratchet pumps and propulsion systems is based on radiometric forces [14]. He was the first researcher to use these pumps for rarefied gas species separation [15]. This topic is exciting in MEMS/NEMS (Micro/nano-electro-mechanical systems) and aerospace communities and impacts technological developments in both fields. The former seeks extra-small scale pumps for miniaturized devices, while the latter is interested in propulsion systems for space applications, like thrust production for space vehicles and orbit control of lightweight satellites.
In addition to his research in rarefied gas dynamics, he works on bio-inspired techniques to mitigate the destructive impacts of cavitation on the performance of hydraulic machinery. He recently worked on wavy leading hydrofoils inspired by a particular Humpback whale species [16]. He showed that the cavitation weakens on the modified geometry, delaying the stall. He also used hybrid surface wettability to control the devastating effects of cavitation [17].
Additionally, he works on novel subgrid-scale (SGS) models in the large eddy simulation (LES) approach for turbulent flows. For the first time, various modern SGS, such as modulated gradient (MG) and anisotropic minimum dissipation (AMD) models, were considered, modified, and implemented in the OpenFOAM framework [18],[19].
Scopus Profile: https://www.scopus.com/authid/detail.uri?authorId=24471770600
Scholar Profile: https://scholar.google.com/citations?hl=en&user=AWKLce4AAAAJ&view_op=list_works&sortby=pubdate
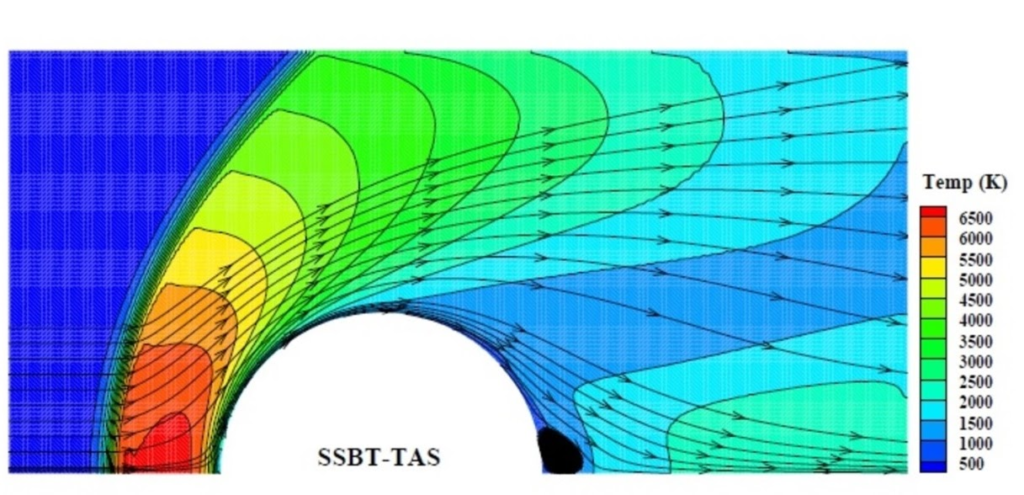
SSBT collision model in predicting the flow field around a hypersonic cylinder, from Roohi’s work in Physics of Fluids, 2015.
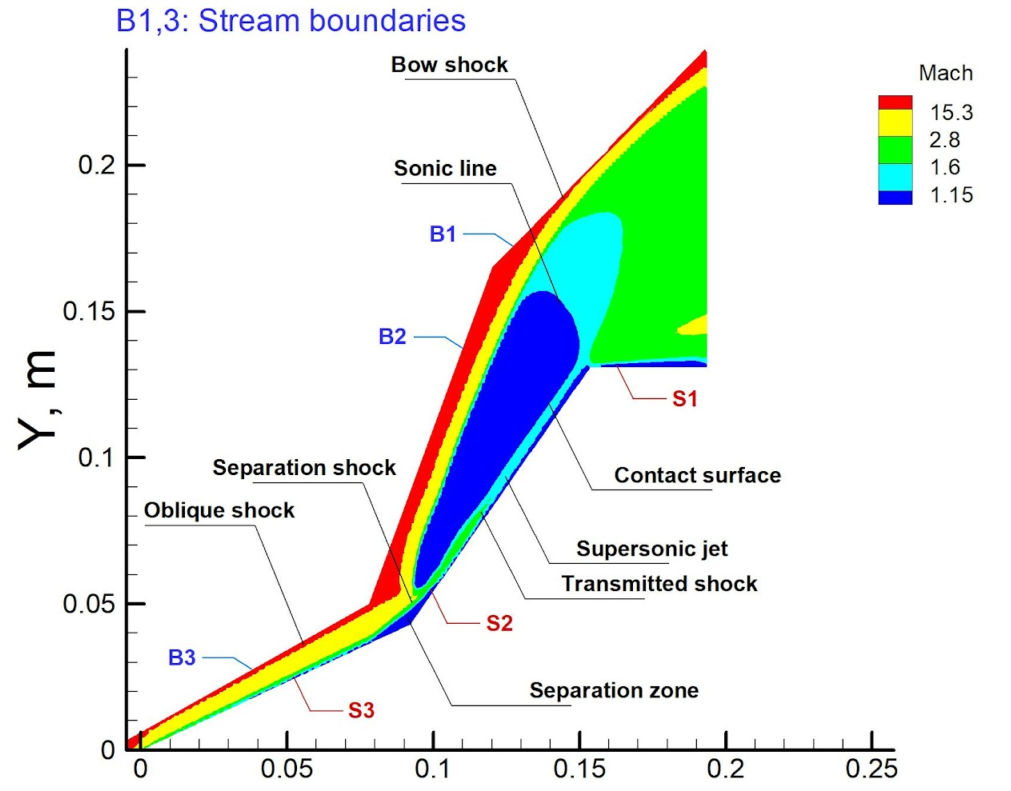
Shock wave structure around the hypersonic biconic geometry, from the Roohi’s work with Stefanov and Goshayeshi, Journal of Computational Physics, 2015.
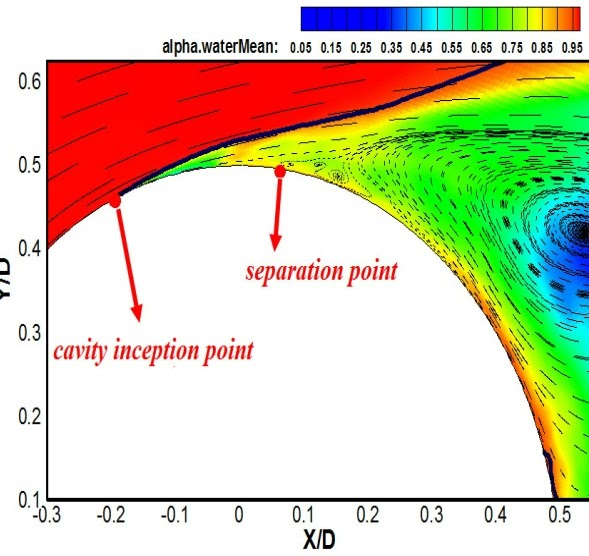
Cavitation around a sphere: Boundary layer separation point (≈96◦) and cavity inception point (≈76◦); velocity vectors are plotted over the mean water volume fraction contour for fluid with the formation of the cavity at a cavitation number of σ=0.45, from Pendar and Roohi’s work in International Journal of Multiphase Flow, 2018.
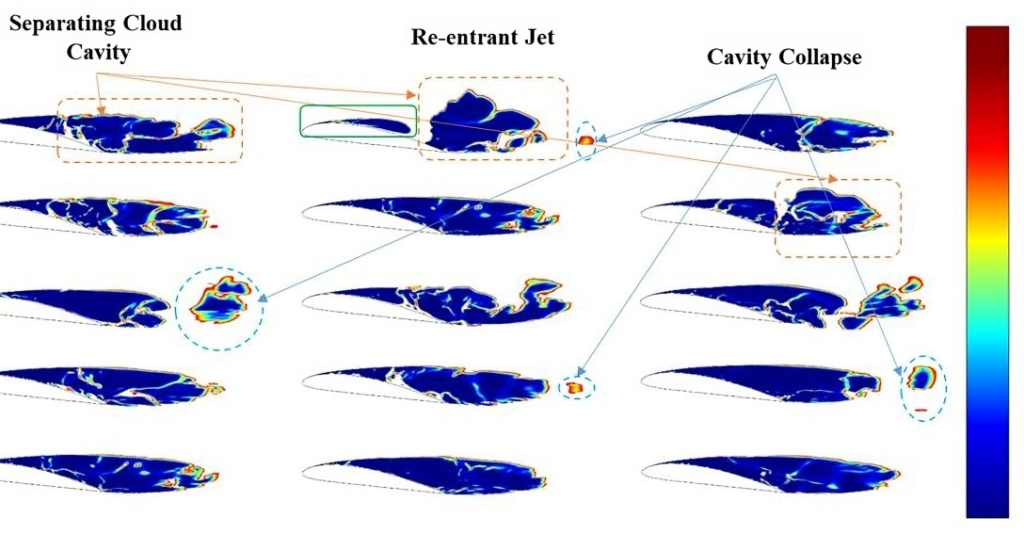
Supercavitating flows around a hydrofoil at a cavitation number of σ=0.4, from Mousavi and Roohi’s work in Journal of the Taiwan Institute of Chemical Engineers, 2023.
Vortex shedding in a rarefied flow behind a cylinder, European Journal of Mechanics – B/Fluids, 2017.
Vortex shedding in a rarefied flow behind a cylinder, , European Journal of Mechanics – B/Fluids, 2017.
Normalized Turbulent Kinetic Energy around a cavitating Pitching-Plunging hydrofoil, from the Alavi and Roohi’s work, Physics of Fluids, 2023.
Cavitation around a wavy leading edge hydrofoil, from Pendar and Roohi’s work published in the International Journal of Multiphase Flow, 2020.
Cavitation around a sphere, Ocean Engineering, 2019.
Temperature field for rarefied flow with a 75 degrees angle towards a flat plate (DSMC Simulation)
Collision Frequency for flow with a 75 degrees angle towards a flat plate (DSMC Simulations)
Density evolution for rarefied flow with a 75 degrees angle towards a flat plate (DSMC Simulations)
A summary of numerical and experimental investigation on the effect of propeller-atomizer distance in presence of crosswind in agricultural UAV based plant protection.
- Geometry: Propeller + Atomizer
- Simulator: Fluent, k-omega SST
- Methodology: Eulerian, Lagrangian
- Species: Air, Water droplets
- Propeller RPM: 11500
- Atomizer RPM: 18500
- Wind speed: 1m/s
Platelet adhesion and aggregation are essential for primary hemostasis, forming a clot that quickly stops initial bleeding. Despite this critical role, the dynamic interactions of platelet receptors with exposed collagen and von Willebrand factor (vWF) at the injury site and how these interactions influence thrombus formation under varying blood flow conditions are not fully understood. This study aimed to investigate the mechanisms of platelet adhesion and aggregation on collagen- or vWF-coated surfaces. We combined the stochastic Bell’s law with a deterministic elastic force featuring a time-dependent coefficient within the context of a dissipative particle dynamics (DPD) model to numerically simulate thrombosis formation. Our simulation results revealed that the numerically predicted platelet adhesion patterns closely matched experimental observations reported in the literature, demonstrating accurate replication of platelet behavior on collagen- and vWF-coated surfaces. Consequently, our deterministic/stochastic force model in DPD provides valuable insights into platelet adhesion dynamics under different flow conditions. These results contribute to a deeper understanding of platelet dynamics and potential therapeutic targets for managing hemostatic disorders.

My research group showed for the first time that the reason of cold-to-hot transfer in the cavity geometry in the rarefied regime is the role of the second derivative of the velocity, see the notes on the left, see our paper in Physical Review E, 2012.
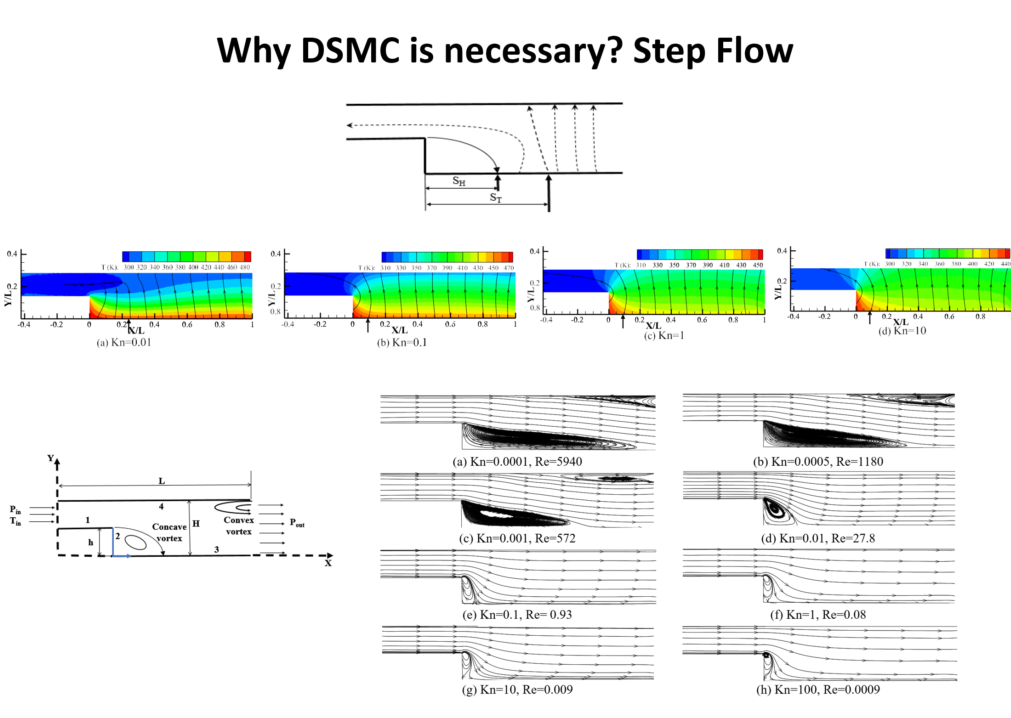
A similar cold to hot transfer (anti-Fourier) was observed in the step geometry. Some of the heat lines near the inlet deflect back and go to the cold region, see our paper in Physics of Fluids in 2015. We also studied step problem at very low Knudsen numbers with molecular approach, and for the first time, we detected the vortices near the top wall of the step at high Re/low Kn conditions (Physics of Fluids, 2022).

In 2021, NASA sent a helicopter to Mars, the mean free path of gas (primarily CO2) on the surface of Mars is approximately 9.82 μm. So, the gas is rarefied. in 2014, we studied flow over airfoils at early slip regimes. The figure at left shows the difference between the vortex structure from DSMC and NS solutions.
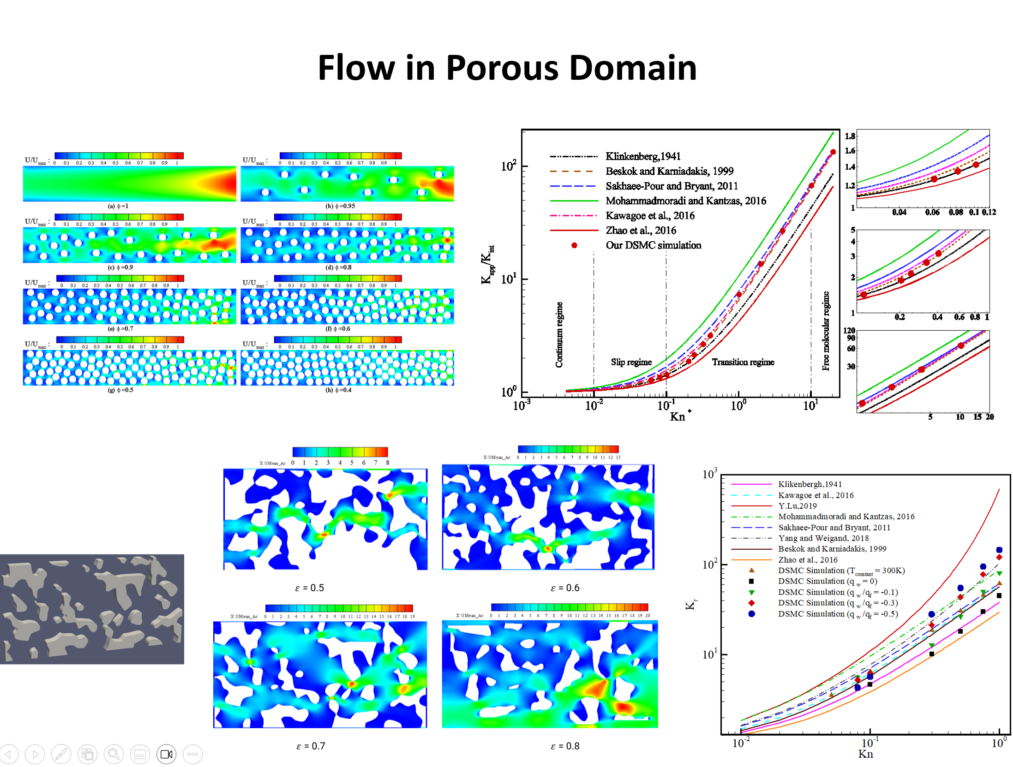
We investigated flow in porous media in rarefied gas using DSMC. The influence of the morphology along with rarefaction and gas type on the apparent permeability is investigated. Moreover, the effects of porosity, solid particle’s diameter and specific surface area are considered. Our results demonstrate that although decreasing porosity intensifies tortuosity in the flow field, the tortuosity reduces at higher Knudsen numbers due to slip flow at solid boundaries. In addition, our study on two different gas species showed that the gas type affects slippage and apparent gas permeability. Comparing different apparent permeability models showed that Beskok and Karniadakis model is valid only up to the early transition regime and at higher Knudsen numbers, the current data matches those models that take Knudsen diffusion into account as well.

The timeline illustrates the progress of collision models in DSMC, starting with G. Bird’s introduction of the No-Time-Counter Collision Scheme (NTC) in 1989, which optimized computational efficiency by simplifying collision pair selection based on proximity. In 1990, Yanitskiy developed the Bernoulli Trial (BT) collision model, introducing hierarchical sorting to reduce the error of repeated collisions. In 2011, Stefanov proposed the Simplified Bernoulli Trial (SBT) model, streamlining the BT scheme to further enhance efficiency. In 2015, Goshayeshi et al. in Roohi’s group introduced the Intelligent Simplified Bernoulli Trial (ISBT) and SBT-TAS (Simplified Bernoulli Trial on transient adaptive sub-cells), improving collision accuracy and time resolution. By 2018, Roohi et al. developed the Generalized Bernoulli Trial (GBT) model, which provided greater adaptability to diverse flow conditions, such as hypersonic and microscale flows. In 2022, Taheri et al. in Roohi’s group presented the Symmetrized Simplified Bernoulli Trial (SSBT), focusing on simplicity and efficiency. Stefanov and colleagues introduced a Hybrid Collision Model on the same year. Most recently, in 2024, Javani et al. (from Roohi’s group) developed the Simplified Generalized Bernoulli Trial (SGBT) model, merging the strengths of GBT and SSBT to deliver high accuracy and computational efficiency for DSMC simulations in complex geometries. These advancements highlight a continuous drive done in Roohi’s group for more efficient, accurate, and adaptable collision models tailored to evolving simulation demands.

This figure shows the history of developed collision models in Roohi’s group, and how the BT, SBT and SSBT differ. BT considers all the particles in the list after the first particle and check their collision probability. SBT just considers one particle in the list after the first particle, while SSBT considers the particles before the first-chosen particle as well. This is detailed in the figure on the right side.

This figure shows the SGBT procedure, Javani et al. 2024. SGBT considers N_sel number of particles and perform SSBT procedure just for this N_Sel particles. The collision probability formula for SGBT was detailed in Javani et al. paper.
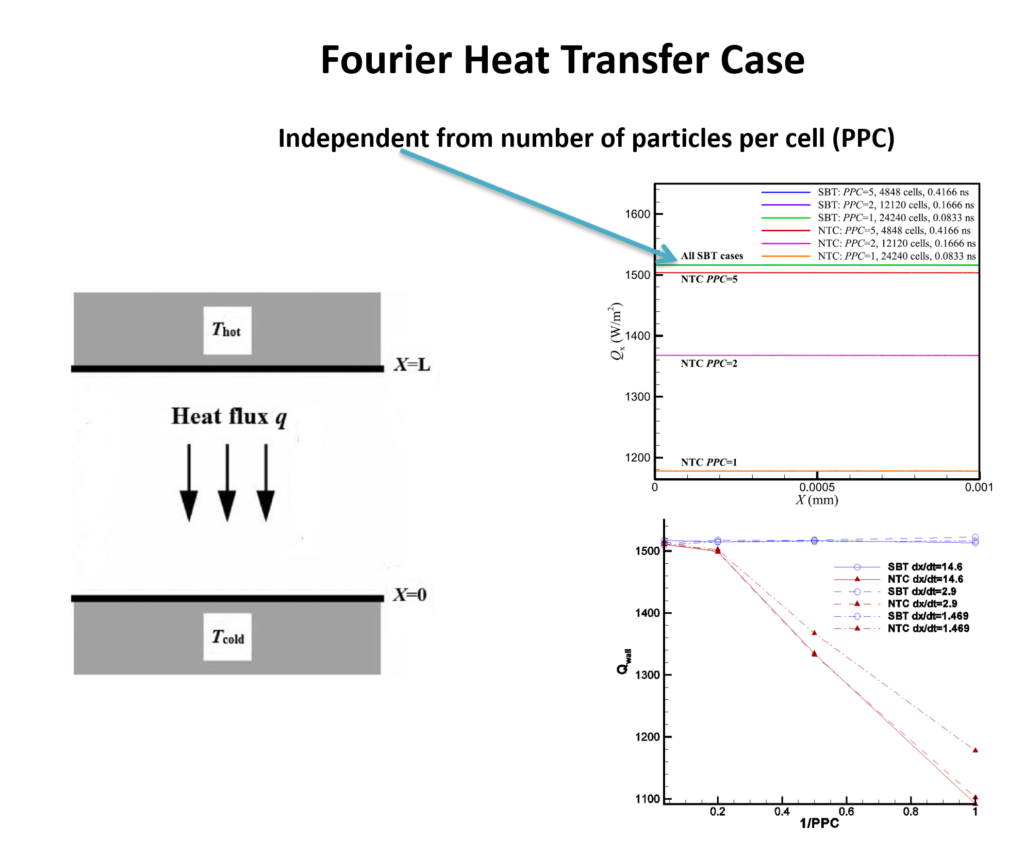
The figure shows that SBT collision family could capture heat transfer between two plates just with one particle per cell, while NTC, developed by Bird, fails to do so and needs higher particle per cell (PPC). SBT results show independence from number of PPC. This is detailed in our 2016 work in Physics of Fluids.
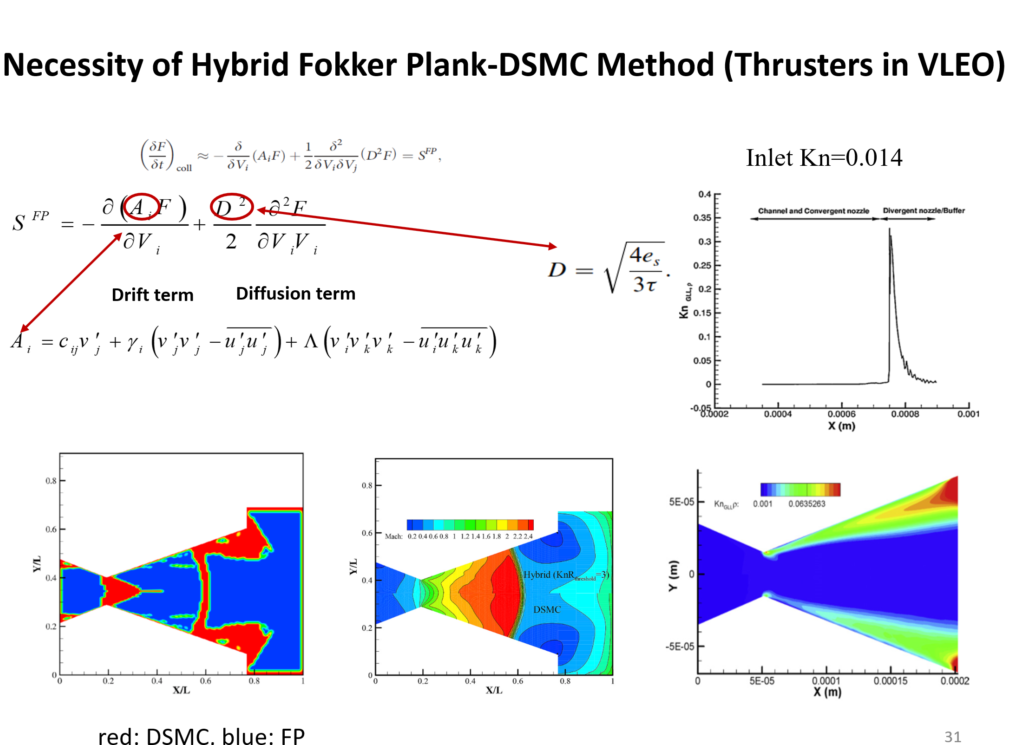
We used a hybrid DSMC-Fokker Plank (FP) approach for nozzle flow simulations, the red regions, i.e., throat and shock regions, were modeled by DSMC, while the other regions were simulated with FP. See our paper in Vacuum, 2020.
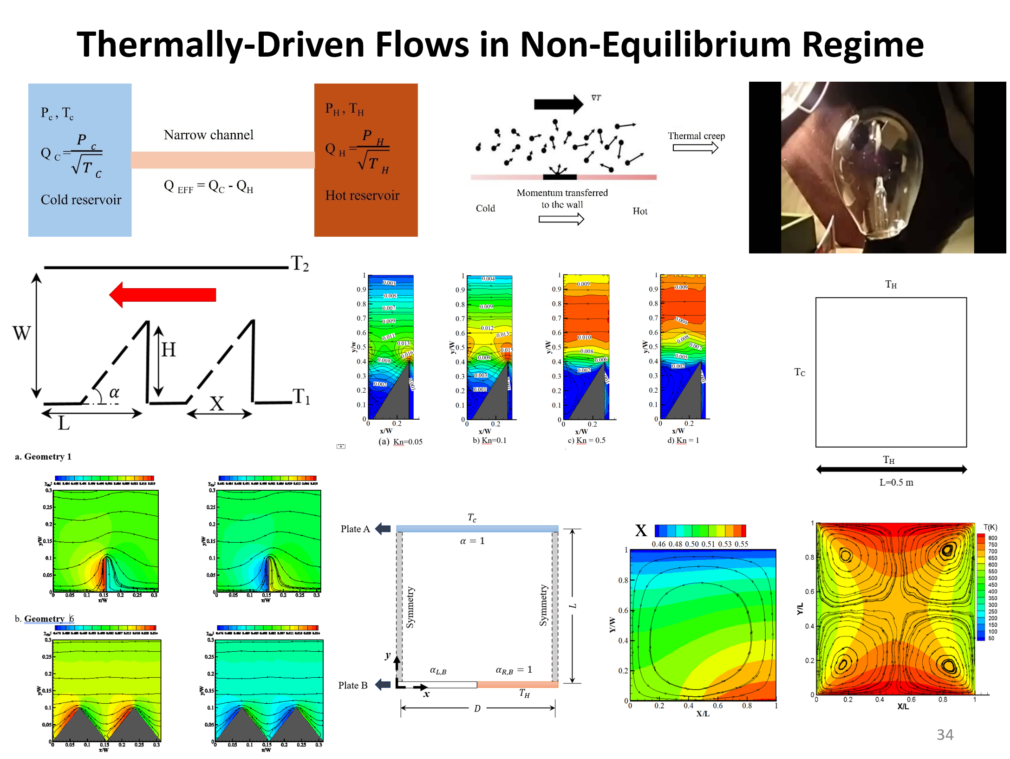
In rarefied gas, temperature difference can induce flow. The figure shows various thermally-driven flows induced in different geometries, i.e., ratchet, vane and cavity. The ratchet can induce flow and also can perform species separation. The species separation is also observed in the cavity geometry, see our papers in Journal of Fluid Mechanics (2019), International Communication in Heat and Mass Transfer (2021, 2025), and Fluids (2022).
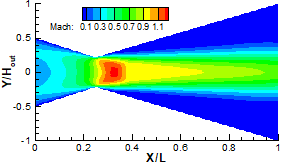
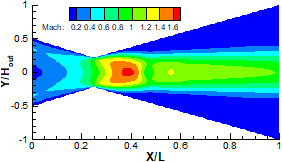
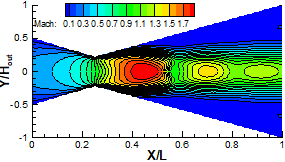
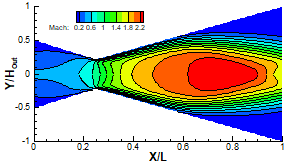
DSMC solution of the Mach number maps at different back pressures for viscous wall. The figures show a series of diamond shocks.
a) Pb=35 KPa
b) Pb=25 KPa
c) Pb=15 KPa
d) Pb=7 KPa
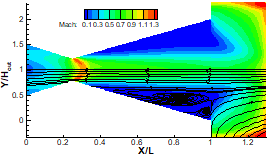

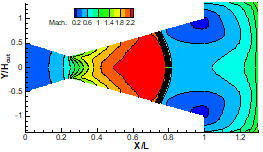
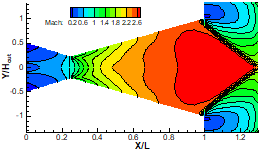
DSMC solution of the Mach number contours in nozzle with different back pressures and with inviscid wall. Diamond shocks in the previous figures are converted to bow shocks or oblique shocks.
a) Pb=35 KPa
b) Pb=25 KPa
c) Pb=15 KPa
d) Pb=7 KPa
3. ^ “Direct simulation Monte Carlo”.
4. ^ Roohi, Ehsan; Stefanov, Stefan (2016). “Collision partner selection schemes in DSMC: From micro/Nano flows to hypersonic flows”. Physics Reports. 656: 1–38. Bibcode:2016PhR…656….1R. doi:10.1016/j.physrep.2016.08.002.
5. ^ Akhlaghi, Hassan; Roohi, Ehsan; Stefanov, Stefan (2018). “On the consequences of successively repeated collisions in no-time-counter collision scheme in DSMC”. Computers & Fluids. 161: 23–32. doi:10.1016/j.compfluid.2017.11.005.
6. ^ Stefanov, Stefan K. (January 25, 2011). “On DSMC Calculations of Rarefied Gas Flows with Small Number of Particles in Cells”. SIAM Journal on Scientific Computing. 33 (2): 677–702. Bibcode:2011SJSC…33..677S. doi:10.1137/090751864 – via CrossRef.
7. ^ https://pubs.aip.org/aip/pof/article-abstract/27/10/107104/314632/A-novel-simplified-Bernoulli-trials-collision?redirectedFrom=fulltext
8. ^ Roohi, Ehsan; Stefanov, Stefan; Shoja-Sani, Ahmad; Ejraei, Hossein (2018). “A generalized form of the Bernoulli Trial collision scheme in DSMC: Derivation and evaluation”. Journal of Computational Physics. 354: 476–492. Bibcode:2018JCoPh.354..476R. doi:10.1016/j.jcp.2017.10.033.
9. ^ https://pubs.aip.org/aip/pof/article-abstract/34/1/012010/2845513/A-symmetrized-and-simplified-Bernoulli-trial
10. ^ https://pubs.aip.org/aip/pof/article-abstract/34/9/092003/2844541/A-novel-transient-adaptive-subcell-algorithm-with?redirectedFrom=fulltext
11. ^ Goshayeshi, Bijan; Roohi, Ehsan; Stefanov, Stefan (2015). “DSMC simulation of hypersonic flows using an improved SBT-TAS technique”. Journal of Computational Physics. 303: 28–44. Bibcode:2015JCoPh.303…28G. doi:10.1016/j.jcp.2015.09.027.
12. ^ Scanlon, T.J.; Roohi, E.; White, C.; Darbandi, M.; Reese, J.M. (2010). “An open source, parallel DSMC code for rarefied gas flows in arbitrary geometries”. Computers & Fluids. 39 (10): 2078–2089. doi:10.1016/j.compfluid.2010.07.014.
13. ^ https://www.cambridge.org/core/journals/journal-of-fluid-mechanics/article/abs/radiometric-flow-in-periodically-patterned-channels-fluid-physics-and-improved-configurations/DA76621385D7DF0C3824B8D3F215FE13
14. ^ https://www.nature.com/articles/srep41412
15. ^ https://www.sciencedirect.com/science/article/abs/pii/S0735193320305881
16. ^ https://www.sciencedirect.com/science/article/abs/pii/S0301932220305243
17. ^ https://www.sciencedirect.com/science/article/abs/pii/S1876107023001578
18. ^ https://www.tandfonline.com/doi/abs/10.1080/14685248.2018.1483078
19. ^ https://www.sciencedirect.com/science/article/abs/pii/S0045793018309368